特殊溫度下材料阻隔性參數的獲得方法 ——阻隔性參數擬合

    眾所周知溫度對阻隔性測試的影響是十分顯著的，溫度的波動能夠引起阻隔性能的大幅度變化。要想准確、科學地獲得在某溫度下的阻隔性數據，最常規的處理方法就是在該溫度下進行實際測試。但現實中，檢測設備的使用溫度范圍常常不能滿足這種要求，那麼如何纔能准確、科學地獲得這些溫度下的阻隔性數據呢？現在可以采用阻隔性參數擬合算法來實現。

1、阻隔性參數擬合

    擬合是求解離散數據逼近函數的一種數學計算方法。阻隔性參數擬合，簡單的說就是通過試驗，獲得在容易實現的溫度條件下的試驗數據，然後通過擬合算法，求得特殊溫度下的阻隔性參數值的數學計算過程。

2、阻隔性參數擬合的理論依據

    無機氣體的滲透系數、擴散系數、溶解度系數與溫度的關系均服從 Arrhenius 方程 [1 － 2] ：

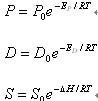
式中： P、D、S ——滲透系數、擴散系數、溶解度系數

Po、Do、So ——與氣體－固體配偶有關的常數

E P、E D、ΔH ——透過活化能、擴散活化能、溶解熱

R ——摩爾氣體常數， 8.31441J/mol·K

T ——絕對溫度

    對於常見無機氣體，溫度昇高， P、D、S 增大，溫度波動明顯影響測試結果。

3、Labthink VAC-V1 的阻隔性參數擬合功能

    Labthink 最新推出的 VAC-V1 氣體滲透儀，具備阻隔性參數擬合的功能。通過使用 VAC-V1 試驗，獲得可實現溫度范圍內 2 組以上不同溫度的試驗數據時，使用者就可以使用設備自帶的擬合功能輕松獲得指定溫度下的氣體滲透量、滲透系數、擴散系數以及溶解系數。實測試驗數據越多，擬合結果越准確。由於 VAC-V1 具有 5℃～ 50℃的測試溫度自控溫功能，這就使得對於阻隔性參數擬合功能的使用更加簡單、方便。

    現使用 VAC-V1 進行 125 μm 厚的 PC 膜的氧氣滲透性測試，在 30℃、35℃、40℃下進行試驗，得到以下試驗數據（見表 1）。

表 1. PC 膜測試數據

    由以上數據擬合得到 45℃的 O₂ 滲透系數是 16.04 × 10 -11 cm³·cm/m²·s·cmHg，O₂ 滲透量是 842.85cm³/m²·24h·0.1MPa，實際的測試結果是 15.79 × 10 -11 cm³·cm/m²·s·cmHg 和 829.729cm³/m²·24h·0.1MPa，預測值與測量值的誤差僅有 1.58％，很理想。當然了，擬合功能對材料是沒有選擇性的，對於其它薄膜，使用原理都一樣。

    VAC-V1 還能將某段溫度范圍內的擬合值導入 Excel 文件，方便使用者對於一系列數據進行分析處理。現將由 3 組試驗數據擬合得到的－100℃ ～ 120℃（173 ～ 393K）的 PC 膜氧氣透過量（以透過量為例）導入 Excel 並作圖，可得圖 1。另外，設備還可以對極限溫度以內的所有溫度點進行擬合統計，使用者可以很容易地了解到在整個溫度范圍內阻隔性參數隨溫度的變化趨勢。

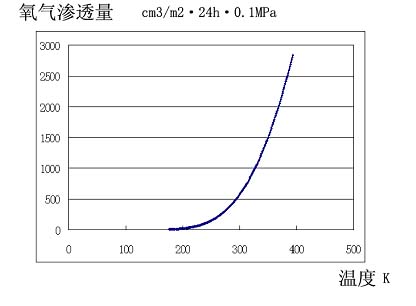
圖 1. PC 膜氧氣滲透量與溫度的曲線

4、聚合物玻璃態轉化溫度

    非結晶體聚合物存在兩種形態，其一為玻璃態，此間分子運動很受限制，就像凍結於體系中；另一為橡膠態，這時分子可作長距離的運動，而不存在永久性的孔隙。這種由常溫“玻璃態”轉變成物性明顯不同的高溫“橡膠態”的過程中狹窄的溫變過度區域被稱為“玻璃態轉化溫度”（Tg）。當 T>Tg 時，聚合物的結構會發生蠕變而受到破壞，因此在 Tg 上下，擴散分子運動情況不同，阻隔系數 ~1/T 曲線走勢在 Tg 附近出現了明顯的轉折。

5、展望

    對於常見無機氣體的滲透， VAC-V1 的擬合功能是獲得特殊溫度下 P、D、S 值的有效途徑。隨著科技的發展，可用於得到特殊溫度下 P、D、S 值的方法會逐漸增多，理論上的一些經驗公式也會得到進一步的修正，同時測試技術的昇級也能提供更加寬廣的測試環境溫度，這些都為獲得特殊溫度下的非標試驗阻隔性參數提供了更多的有利條件。